Toroidal coordinates: Difference between revisions
| Line 36: | Line 36: | ||
<ref>Morse and Feshbach, ''Methods of theoretical physics'', McGraw-Hill, New York, 1953 ISBN 007043316X</ref> | <ref>Morse and Feshbach, ''Methods of theoretical physics'', McGraw-Hill, New York, 1953 ISBN 007043316X</ref> | ||
<ref>[[:Wikipedia:Toroidal coordinates]]</ref> | <ref>[[:Wikipedia:Toroidal coordinates]]</ref> | ||
:<math>R = R_p \frac{\sinh \zeta}{\cosh \zeta - \cos \eta}</math> | :<math>R = R_p \frac{\sinh \zeta}{\cosh \zeta - \cos \eta}</math> | ||
| Line 48: | Line 46: | ||
The coordinate ''η'' is a poloidal angle and runs from 0 to 2π. | The coordinate ''η'' is a poloidal angle and runs from 0 to 2π. | ||
This system is orthogonal. | This system is orthogonal. | ||
The Laplace equation separates in this system of coordinates, thus allowing an expansion of the vacuum magnetic field in toroidal harmonics. | |||
<ref>F. Alladio, F. Chrisanti, ''Analysis of MHD equilibria by toroidal multipolar expansions'', Nucl. Fusion '''26''' (1986) 1143</ref> | |||
<ref>[http://dx.doi.org/10.1016/0010-4655(94)90112-0 B.Ph. van Milligen and A. Lopez Fraguas, ''Expansion of vacuum magnetic fields in toroidal harmonics'', Computer Physics Communications '''81''', Issues 1-2 (1994) 74-90]</ref> | |||
== Magnetic == | == Magnetic == | ||
Revision as of 11:49, 15 September 2009
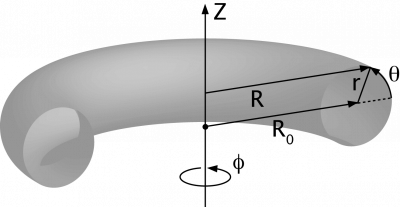
Coordinate systems used in toroidal systems:
Cartesian
(X, Y, Z) [1]
Cylindrical
(R, φ, Z), where [2]
- R2 = X2 + Y2, and
- tan φ = Y/X.
φ is called the toroidal angle (and not the cylindrical angle, at least not in the context of magnetic confinement).
Cylindrical symmetry (symmetry under rotation over φ) is referred to as axisymmetry.
Simple toroidal
(r, φ, θ), where
- R = R0 + r cos θ, and
- Z = r sin θ
R0 corresponds to the torus axis and is called the major radius, while r is called the minor radius, and θ the poloidal angle.
In order to adapt this simple system better to the magnetic surfaces of an axisymmetric MHD equilibrium, it may be enhanced by [3]
- letting R0 depend on r (to account for the Shafranov shift of flux surfaces)
- adding ellipticity (ε), triangularity (κ), etc. (to account for non-circular flux surface cross sections)
Toroidal
where Rp is the pole of the coordinate system. Surfaces of constant ζ are tori with major radii R = Rp/tanh ζ and minor radii r = Rp/sinh ζ. At R = Rp, ζ = ∞, while at infinity and at R = 0, ζ = 0. The coordinate η is a poloidal angle and runs from 0 to 2π. This system is orthogonal.
The Laplace equation separates in this system of coordinates, thus allowing an expansion of the vacuum magnetic field in toroidal harmonics. [6] [7]
Magnetic
All of the above coordinate systems are fixed and axisymmetric (except the Cartesian system). By contrast, magnetic coordinates adapt to the magnetic field, and therefore to the MHD equilibrium (also see Flux surface). Magnetic coordinates simplify the description of the magnetic field. In 3 dimensions (not assuming axisymmetry), the most commonly used coordinate systems are: [8]
- Hamada coordinates. [9][10] In these coordinates, both the field lines and current lines corresponding to the MHD equilibrium are straight.
- Boozer coordinates. [11][12] In these coordinates, the field lines corresponding to the MHD equilibrium are straight.
These two coordinate systems are related. [13]
References
- ↑ Wikipedia:Cartesian coordinate system
- ↑ Wikipedia:Cylindrical coordinate system
- ↑ R.L. Miller et al, Noncircular, finite aspect ratio, local equilibrium model, Phys. Plasmas 5 (1998) 973
- ↑ Morse and Feshbach, Methods of theoretical physics, McGraw-Hill, New York, 1953 ISBN 007043316X
- ↑ Wikipedia:Toroidal coordinates
- ↑ F. Alladio, F. Chrisanti, Analysis of MHD equilibria by toroidal multipolar expansions, Nucl. Fusion 26 (1986) 1143
- ↑ B.Ph. van Milligen and A. Lopez Fraguas, Expansion of vacuum magnetic fields in toroidal harmonics, Computer Physics Communications 81, Issues 1-2 (1994) 74-90
- ↑ W.D. D'haeseleer, Flux coordinates and magnetic field structure: a guide to a fundamental tool of plasma theory, Springer series in computational physics, Springer-Verlag (1991) ISBN 3540524193
- ↑ S. Hamada, Nucl. Fusion 2 (1962) 23
- ↑ J.M. Greene and J.L Johnson, Stability Criterion for Arbitrary Hydromagnetic Equilibria, Phys. Fluids 5 (1962) 510
- ↑ A.H. Boozer, Plasma equilibrium with rational magnetic surfaces, Phys. Fluids 24 (1981) 1999
- ↑ A.H. Boozer, Establishment of magnetic coordinates for a given magnetic field, Phys. Fluids 25 (1982) 520
- ↑ K. Miyamoto, Controlled fusion and plasma physics, Vol. 21 of Series in Plasma Physics, CRC Press (2007) ISBN 1584887095