Toroidal coordinates
Coordinate systems used in toroidal systems:
Cartesian coordinates
(X, Y, Z) [1]
Cylindrical coordinates
, where [2]
- , and
- .
is called the toroidal angle (and not the cylindrical angle, at least not in the context of magnetic confinement).
Cylindrical symmetry (symmetry under rotation over ) is referred to as axisymmetry.
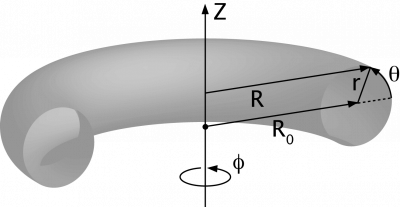
Simple toroidal coordinates
, where
- , and
corresponds to the torus axis and is called the major radius, while is called the minor radius, and θ the poloidal angle. The ratio is called the aspect ratio of the torus.
In order to adapt this simple system better to the magnetic surfaces of an axisymmetric MHD equilibrium, it may be enhanced by [3]
- letting depend on (to account for the Shafranov shift of flux surfaces) [4]
- adding ellipticity (), triangularity (), and squareness () to account for non-circular flux surface cross sections. A popular simple expression for shaped flux surfaces is: [5]
Warning: there are varying conventions for the directions of and . Which convention is used can depend on the local facility, the software being used, or other context. To help reduce confusion, the different tokamak coordinate conventions have been described and codified in the COCOS system.[6]
Toroidal coordinates
where is the pole of the coordinate system. Surfaces of constant are tori with major radii and minor radii . At , , while at infinity and at . The coordinate is a poloidal angle and runs from 0 to . This system is orthogonal.
The Laplace equation separates in this system of coordinates, thus allowing an expansion of the vacuum magnetic field in toroidal harmonics. [9] [10]
Magnetic coordinates
Magnetic coordinates are a particular type of flux coordinates in which the magnetic field lines are straight lines. Magnetic coordinates adapt to the magnetic field, and therefore to the MHD equilibrium (also see Flux surface). Magnetic coordinates simplify the description of the magnetic field. In 3 dimensions (not assuming axisymmetry), the most commonly used coordinate systems are: [11]
- Hamada coordinates. [12][13] In these coordinates, both the field lines and current lines corresponding to the MHD equilibrium are straight.
- Boozer coordinates. [14][15] In these coordinates, the field lines corresponding to the MHD equilibrium are straight and so are the diamagnetic lines , i.e. the integral lines of .
These two coordinate systems are related. [16]
References
- ↑ Wikipedia:Cartesian coordinate system
- ↑ Wikipedia:Cylindrical coordinate system
- ↑ R.L. Miller et al, Noncircular, finite aspect ratio, local equilibrium model, Phys. Plasmas 5 (1998) 973
- ↑ R.D. Hazeltine, J.D. Meiss, Plasma confinement, Courier Dover Publications (2003) ISBN 0486432424
- ↑ R.L. Miller, M.S. Chu, J.M. Greene, Y.R. Lin-Liu and R.E. Waltz, Noncircular, finite aspect ratio, local equilibrium model, Phys. Plasmas 5 (1998) 973
- ↑ O. Sauter and S.Yu. Medvedev, Tokamak coordinate conventions: COCOS, Computer Physics Communications 184, (2013) 293-302
- ↑ Morse and Feshbach, Methods of theoretical physics, McGraw-Hill, New York, 1953 ISBN 007043316X
- ↑ Wikipedia:Toroidal coordinates
- ↑ F. Alladio, F. Crisanti, Analysis of MHD equilibria by toroidal multipolar expansions, Nucl. Fusion 26 (1986) 1143
- ↑ B.Ph. van Milligen and A. Lopez Fraguas, Expansion of vacuum magnetic fields in toroidal harmonics, Computer Physics Communications 81, Issues 1-2 (1994) 74-90
- ↑ W.D. D'haeseleer, Flux coordinates and magnetic field structure: a guide to a fundamental tool of plasma theory, Springer series in computational physics, Springer-Verlag (1991) ISBN 3540524193
- ↑ S. Hamada, Nucl. Fusion 2 (1962) 23
- ↑ J.M. Greene and J.L Johnson, Stability Criterion for Arbitrary Hydromagnetic Equilibria, Phys. Fluids 5 (1962) 510
- ↑ A.H. Boozer, Plasma equilibrium with rational magnetic surfaces, Phys. Fluids 24 (1981) 1999
- ↑ A.H. Boozer, Establishment of magnetic coordinates for a given magnetic field, Phys. Fluids 25 (1982) 520
- ↑ K. Miyamoto, Controlled fusion and plasma physics, Vol. 21 of Series in Plasma Physics, CRC Press (2007) ISBN 1584887095