TJ-II:Turbulence: Difference between revisions
No edit summary |
|||
| Line 6: | Line 6: | ||
Our work on turbulence has focussed mainly on the analysis of edge [[TJ-II:Langmuir Probes|Langmuir probe]] data, although some analysis was done on other types of data (e.g., [[TJ-II:Reflectometry|reflectometry]] signals). Much effort was devoted to the development of new analysis techniques. | Our work on turbulence has focussed mainly on the analysis of edge [[TJ-II:Langmuir Probes|Langmuir probe]] data, although some analysis was done on other types of data (e.g., [[TJ-II:Reflectometry|reflectometry]] signals). Much effort was devoted to the development of new analysis techniques. | ||
=== | === Bicoherence and wavelets === | ||
[[File:Bicoherence.png|300px|thumb|right|Auto-[[Bicoherence|bicoherence]] graph (''E<sub>θ</sub>'') during a spontaneous confinement transition at TJ-II, showing the coupling of high to low frequencies (horizontal and diagonal lines), i.e., a possible inverse spectral cascade. (from B.Ph. van Milligen et al, Nucl. Fusion 48 (2008) 115003)]] | [[File:Bicoherence.png|300px|thumb|right|Auto-[[Bicoherence|bicoherence]] graph (''E<sub>θ</sub>'') during a spontaneous confinement transition at TJ-II, showing the coupling of high to low frequencies (horizontal and diagonal lines), i.e., a possible inverse spectral cascade. (from B.Ph. van Milligen et al, Nucl. Fusion 48 (2008) 115003)]] | ||
Turbulence is essentially non-linear. | Turbulence is essentially non-linear. | ||
Non-linear interactions can be detected by means of higher-order spectra (e.g. quadratic interactions can be detected through the bi-spectrum). With Fourier analysis, however, in order to achieve statistically significant values for the bi-spectrum, very long time series are necessary. This fact has mostly precluded its use in fields like plasma turbulence, since long steady-state data series are not generally available. In our work, for the first time, the bicoherence was calculated using wavelet transforms, thus making the detection of non-linear interactions with time resolution possible. | Non-linear interactions can be detected by means of higher-order spectra (e.g. quadratic interactions can be detected through the bi-spectrum). With Fourier analysis, however, in order to achieve statistically significant values for the bi-spectrum, very long time series are necessary. This fact has mostly precluded its use in fields like plasma turbulence, since long steady-state data series are not generally available. In our work, for the first time, the [[Bicoherence|bicoherence]] was calculated using wavelet transforms, thus making the detection of non-linear interactions with time resolution possible. | ||
<ref>[http://link.aps.org/doi/10.1103/PhysRevLett.74.395 B.Ph. van Milligen et al, ''Nonlinear phenomena and intermittency in plasma turbulence'', Phys. Rev. Lett. '''74''', 3 (1995) 395]</ref> | <ref>[http://link.aps.org/doi/10.1103/PhysRevLett.74.395 B.Ph. van Milligen et al, ''Nonlinear phenomena and intermittency in plasma turbulence'', Phys. Rev. Lett. '''74''', 3 (1995) 395]</ref> | ||
<ref>[http://link.aip.org/link/?PHPAEN/2/3017/1 B.Ph. van Milligen et al, ''Wavelet bicoherence: a new turbulence analysis tool'', Phys. Plasmas '''2''', 8 (1995) 3017]</ref> | <ref>[http://link.aip.org/link/?PHPAEN/2/3017/1 B.Ph. van Milligen et al, ''Wavelet bicoherence: a new turbulence analysis tool'', Phys. Plasmas '''2''', 8 (1995) 3017]</ref> | ||
Revision as of 10:14, 25 September 2010
Transport in fusion-grade plasmas is often dominated by turbulent transport. In contrast with Neoclassical transport, turbulent transport (assumed to be the cause of the experimental so-called "anomalous" component of transport) is not well understood. As a consequence, predictions of machine performance generally rely on rather crude scaling law techniques, rather than first-principles calculations. Improving our understanding of turbulence is hard, due to (1) the complexity of fusion-grade plasmas (the presence of charged particles and magnetic fields make this into a much harder topic than fluid turbulence), (2) the enormous variety of plasma instabilities, and (3) the difficulty of diagnosing the plasma due to the hostile conditions inside the plasma.
Our work on turbulence has focussed mainly on the analysis of edge Langmuir probe data, although some analysis was done on other types of data (e.g., reflectometry signals). Much effort was devoted to the development of new analysis techniques.
Bicoherence and wavelets
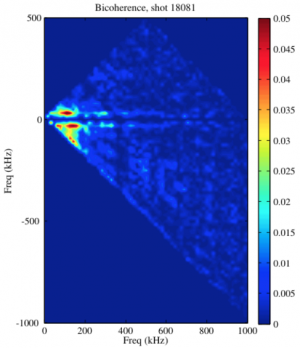
Turbulence is essentially non-linear. Non-linear interactions can be detected by means of higher-order spectra (e.g. quadratic interactions can be detected through the bi-spectrum). With Fourier analysis, however, in order to achieve statistically significant values for the bi-spectrum, very long time series are necessary. This fact has mostly precluded its use in fields like plasma turbulence, since long steady-state data series are not generally available. In our work, for the first time, the bicoherence was calculated using wavelet transforms, thus making the detection of non-linear interactions with time resolution possible. [1] [2] [3] [4] A relation was found between confinement transitions and an increase of the bicoherence, as expected in the framework of shear/zonal flow models for turbulence stabilisation. [5]
Self-similarity
Important transport phenomena such as profile stiffness (consistency), [6] power degradation, the rapid propagation of perturbations, [7] and the Bohm scaling of plasma confinement might be explained on the basis of profile self-regulation in the framework of the Self-Organised Criticality paradigm. This paradigm predicts that transport is regulated by avalanches, which would generate self-similar behaviour in space and time of the turbulent data.
In order to test this hypothesis, one can determine the shape of the autocorrelation function (ACF) of turbulent signals. [8] [9] [10] [11] [12] [13]
Unfortunately, the most revealing information is present in the tail of the distribution (i.e., well beyond the correlation time), where statistics are generally poor. Therefore, it is convenient to resort to the Rescaled-Range analysis technique and the determination of the Hurst exponent. We have shown that this type of analysis is far more robust with respect to random noise perturbations than the direct determination of the ACF or the Probability of Return.
The analysis of data from Langmuir probes taken at the plasma edge in a wide variety of fusion devices reveals the existence of self-similar behaviour or long-range correlations in all devices studied. The observed variation of the Hurst exponent in the plasma edge, 0.62 < H < 0.75, is small in spite of the variety of devices. [14] On the other hand, the variation of H in the scrape-off layer is much larger. In Wendelstein VII-AS, a slight decrease in H at the sheared flow layer was observed, possibly corresponding to a local decorrelation effect.
The repeated occurrence of values of H differing significantly from the value corresponding to random noise (H = 0.5) in all machines points to a universal aspect of the underlying turbulence. Further, the degree of self-similarity detected implies the existence of long-range correlations (with respect to the correlation time). [15] [16]
In this framework, an important technique is the quiet-time analysis. [17] [18] [19]
Turbulence classification
An important effort has also been made to identify and classify turbulence, [20] [21] [22] to analyse its spectra, [23] [24] [25] and to determine its relation with local plasma parameters (rational surfaces, gradients, electric fields). [26] [27] [28]
Turbulence visualisation
Recently, much effort is being dedicated to the visualization of turbulent structures, and to the corresponding analysis techniques for extracting quantitative information from the images. [29] [30] [31]
References
- ↑ B.Ph. van Milligen et al, Nonlinear phenomena and intermittency in plasma turbulence, Phys. Rev. Lett. 74, 3 (1995) 395
- ↑ B.Ph. van Milligen et al, Wavelet bicoherence: a new turbulence analysis tool, Phys. Plasmas 2, 8 (1995) 3017
- ↑ B.Ph. van Milligen et al, Statistically robust linear and non-linear wavelet analysis applied to plasma edge turbulence, Rev. Sci. Instrum. 68 (1997) 967
- ↑ P.H. Diamond et al, In search of the elusive zonal flow using cross-bicoherence analysis, Phys. Rev. Lett. 84, 12 (2000) 4842
- ↑ B.Ph. van Milligen et al, Bicoherence during confinement transitions in the TJ-II stellarator, Nucl. Fusion 48 (2008) 115003
- ↑ B.Ph. van Milligen et al, Quantifying profile stiffness, Plasma and Fusion Research, 3 (2008) S1070
- ↑ B.Ph. van Milligen et al, Pulse propagation in a simple probabilistic transport model, Nucl. Fusion 47 (2007) 189
- ↑ B.A. Carreras et al, Fluctuation-induced flux at the plasma edge in toroidal devices, Phys. Plasmas 3 (7) (1996) 2664
- ↑ B.A. Carreras et al, Long-range time correlations in plasma edge turbulence, Phys. Rev. Lett. 80, (1998) 4438
- ↑ B.A. Carreras et al, Self-similarity properties of the probability distribution function of turbulence-induced particle fluxes at the plasma edge, Phys. Rev. Lett. 83 (1999) 3653
- ↑ B.A. Carreras, Intermittency of plasma edge fluctuation data: Multifractal analysis, Phys. Plasmas, 7, 8 (2000) 3278
- ↑ C. Hidalgo et al, Empirical similarity in the probability density function of turbulent transport in the edge plasma region in fusion plasmas, Plasma Phys. Control. Fusion 44 (2002) 1557
- ↑ B.Ph. Van Milligen et al, Additional evidence for the universality of turbulent fluctuations and fluxes in the scrape-off layer region of fusion plasmas, Phys. Plasmas 12 (2005) 052507
- ↑ B.A. Carreras et al, Self-similarity of the plasma edge fluctuations, Phys. Plasmas 5, 10 (1998) 3632
- ↑ B.A. Carreras et al, Long-range time dependence in the cross-correlation function, Phys. Plasmas 6, 2 (1999) 485
- ↑ B.A. Carreras et al, Experimental evidence of long-range correlation and self-similarity in plasma fluctuations, Phys. Plasmas 6, 5 (1999) 1885
- ↑ R. Sánchez et al, Quiet-time statistics: A tool to probe the dynamics of self-organized-criticality systems from within the strong overlapping regime, Phys. Rev. E, 66 (2002) 036124
- ↑ R. Sánchez et al, Quiet-time statistics of electrostatic turbulent fluxes from the JET tokamak and the W7-AS and TJ-II stellarators, Phys. Rev. Lett. 90, 185005 (2003)
- ↑ V.E. Lynch et al, Determination of long-range correlation by quiet-time statistics, Phys. Plasmas 12 (2005) 052304
- ↑ E. Sánchez et al, Statistical characterization of fluctuation waveforms in the boundary region of fusion and non-fusion plasmas, Phys. Plasmas 7, 5 (2000) 1408
- ↑ I. García-Cortés et al, Turbulent transport studies in the JET edge plasmas in limiter configuration, Plasma Phys. Control. Fusion 42 (2000) 389
- ↑ C. Hidalgo et al, Intermittency and structures in edge plasma turbulence, Comptes Rendus Physique 7, 6 (2006) 679
- ↑ M. A. Pedrosa et al, Empirical similarity of frequency spectra of the edge plasma fluctuations in toroidal magnetic confinement systems, Phys. Rev. Lett. 82 (1999) 3621
- ↑ B.A. Carreras et al, Characterization of the frequency ranges of the plasma edge fluctuation spectra, Phys. Plasmas 6, 12 (1999) 4615
- ↑ M. A. Pedrosa et al, Studies of spectra of the edge plasma fluctuations in toroidal magnetic confinement systems, J. Plasma Fusion. Res. SERIES, 2 (1999) 77
- ↑ M.A. Pedrosa et al, Role of rational surfaces on fluctuations and transport in the plasma edge of the TJ-II stellarator, Czechoslovak Journal of Physics, 50, 12 (2000) 1463
- ↑ B. Gonçalves et al, Experimental investigation of dynamical coupling between density gradients, radial electric fields and turbulent transport in the JET plasma boundary region, Nucl. Fusion 42 (2002) 1205
- ↑ M.A. Pedrosa et al, Edge turbulence during limiter biasing experiments in the TJ-II stellarator, Czechoslovak Journal of Physics, 53 (2003) 877
- ↑ J. A. Alonso et al, Two-Dimensional Turbulence Analysis Using High-Speed Visible Imaging in TJ-II Edge Plasmas, Fusion Science and Technology 50, 2 (2006) 301
- ↑ J.A. Alonso et al, Impact of different confinement regimes on the two-dimensional structure of edge turbulence, Plasma Phys. Control. Fusion 48 (2006) B465
- ↑ D. Carralero et al, Turbulence studies by fast camera imaging experiments in the TJII stellarator, J. Nucl. Mat. 390-391 (2009) 457