Toroidal coordinates

A toroidal coordinate system

Coordinate systems used in toroidal systems:

Cartesian

(X, Y, Z)

Cylindrical

(R, φ, Z), where

• R² = X² + Y², and
• tan φ = Y/X.

φ is called the toroidal angle (and not the cylindrical angle, at least not in the context of magnetic confinement).

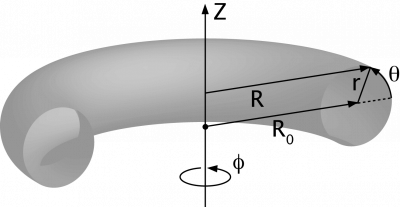
Simple toroidal

(r, φ, θ), where

• R = R₀ + r cos θ, and
• Z = r sin θ

R₀, corresponding to the torus axis, is called the major radius and r the minor radius. θ is called the poloidal angle.

Toroidal

(ζ, η, φ), where

$R=R_{p}{\frac {\sinh \zeta }{\cosh \zeta -\cos \eta }}$

$Z=R_{p}{\frac {\sin \eta }{\cosh \zeta -\cos \eta }}$

where R_p is the pole of the coordinate system. Surfaces of constant ζ are tori with major radii R = R_p/tanh ζ and minor radii r = R_p/sinh ζ. At R = R_p, ζ = ∞, while at infinity and at R = 0, ζ = 0. The coordinate η is a poloidal angle and runs from 0 to 2π. This system is orthogonal.

Magnetic

See Flux surface. All of the above coordinate systems are fixed. By contrast, magnetic coordinates adapt to the magnetic field, and therefore to the MHD equilibrium. Magnetic coordinates simplify the description of the magnetic field (converting them into straight lines in the magnetic coordinate system) or the equilibrium.

• Hamada coordinates
• Boozer coordinates