Toroidal coordinates
Coordinate systems used in toroidal systems:
Cartesian
(X, Y, Z) [1]
Cylindrical
(R, φ, Z), where [2]
- R2 = X2 + Y2, and
- tan φ = Y/X.
φ is called the toroidal angle (and not the cylindrical angle, at least not in the context of magnetic confinement).
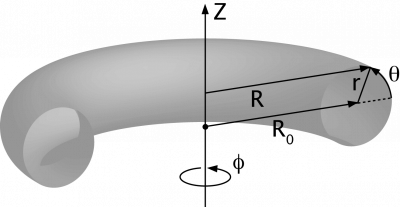
Simple toroidal
(r, φ, θ), where
- R = R0 + r cos θ, and
- Z = r sin θ
R0, corresponding to the torus axis, is called the major radius and r the minor radius. θ is called the poloidal angle.
Toroidal
where Rp is the pole of the coordinate system. Surfaces of constant ζ are tori with major radii R = Rp/tanh ζ and minor radii r = Rp/sinh ζ. At R = Rp, ζ = ∞, while at infinity and at R = 0, ζ = 0. The coordinate η is a poloidal angle and runs from 0 to 2π. This system is orthogonal.
Magnetic
See Flux surface.
References
- ↑ Wikipedia:Cartesian coordinate system
- ↑ Wikipedia:Cylindrical coordinate system
- ↑ Morse and Feshbach, Methods of theoretical physics, McGraw-Hill, New York, 1953 ISBN 007043316X
- ↑ Wikipedia:Toroidal coordinates
- ↑ F. Alladio, F. Chrisanti, Analysis of MHD equilibria by toroidal multipolar expansions, Nucl. Fusion 26 (1986) 1143
- ↑ S. Hamada, Nucl. Fusion 2 (1962) 23
- ↑ J.M. Greene and J.L Johnson, Stability Criterion for Arbitrary Hydromagnetic Equilibria, Phys. Fluids 5 (1962) 510
- ↑ [http://dx.doi.org/10.1063/1.863297 A.H. Boozer, Plasma equilibrium with rational magnetic surfaces, Phys. Fluids 24 (1981) 1999
- ↑ A.H. Boozer, Establishment of magnetic coordinates for a given magnetic field, Phys. Fluids 25 (1982) 520