Toroidal coordinates: Difference between revisions
Jump to navigation
Jump to search
Created page with '400px|thumb|right|A toroidal co-ordinate system Co-ordinate systems used in toroidal systems: == Eulerian == (''X'', ''Y'', ''Z'') == Cylind…' |
|||
| Line 24: | Line 24: | ||
(''ζ'', ''η'', ''φ''), where | (''ζ'', ''η'', ''φ''), where | ||
<ref>Morse and Feshbach, ''Methods of theoretical physics'', McGraw-Hill, New York, 1953 ISBN 007043316X</ref> | <ref>Morse and Feshbach, ''Methods of theoretical physics'', McGraw-Hill, New York, 1953 ISBN 007043316X</ref> | ||
<ref>[[:Wikipedia:Toroidal_coordinates]]</ref> | |||
<ref>F. Alladio, F. Chrisanti, ''Analysis of MHD equilibria by toroidal multipolar expansions'', Nucl. Fusion '''26''' (1986) 1143</ref> | <ref>F. Alladio, F. Chrisanti, ''Analysis of MHD equilibria by toroidal multipolar expansions'', Nucl. Fusion '''26''' (1986) 1143</ref> | ||
Revision as of 11:35, 13 September 2009
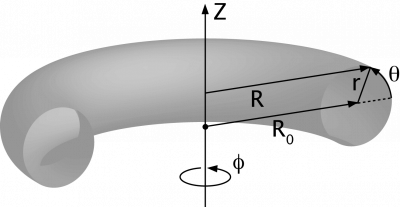
Co-ordinate systems used in toroidal systems:
Eulerian
(X, Y, Z)
Cylindrical
(R, φ, Z), where
- R2 = X2 + Y2, and
- tan φ = Y/X.
Simple toroidal
(r, φ, θ), where
- R = R0 + r cos θ, and
- Z = r sin θ
(R0 corresponding to the axis of the torus)
Toroidal
where Rp is the pole of the coordinate system. Surfaces of constant ζ are tori with major radii R = Rp/tanh ζ and minor radii r = Rp/sinh ζ. At R = Rp, ζ = ∞, while at infinity and at R = 0, ζ = 0. The coordinate η is a poloidal angle and runs from 0 to 2π. This system is orthogonal.
Magnetic
See Flux surface.
References
- ↑ Morse and Feshbach, Methods of theoretical physics, McGraw-Hill, New York, 1953 ISBN 007043316X
- ↑ Wikipedia:Toroidal_coordinates
- ↑ F. Alladio, F. Chrisanti, Analysis of MHD equilibria by toroidal multipolar expansions, Nucl. Fusion 26 (1986) 1143