Ellipticity: Difference between revisions
Jump to navigation
Jump to search
No edit summary |
Add a figure with simple illustrations of Shafranov shift, elongation, triangularity, and squareness. |
||
| (4 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
[[File:Geometry.png|400px|thumb|right|Sketch of tokamak geometry]] | [[File:Geometry.png|400px|thumb|right|Sketch of tokamak geometry]] | ||
The ellipticity refers to the shape of the poloidal cross section of the Last Closed [[Flux surface]] or [[separatrix]] of a [[tokamak]]. | [[File:Cross_section_1shift_2elong_3triang_4square.png|400px|thumb|right|Illustration of the m=1,2,3, and 4 perturbations to a tokamak plasma cross section. Ellipticity/elongation is the m=2 perturbation (second from the left).]] | ||
The ellipticity (also referred to as elongation<ref name="Luce2013">T.C. Luce, [[doi:10.1088/0741-3335/55/9/095009|Plasma Phys. Control. Fusion '''55''' (2013) 095009 ]]</ref>) refers to the shape of the poloidal cross section of the Last Closed [[Flux surface]] or [[separatrix]] of a [[tokamak]]. | |||
Assuming<ref name="Luce2013" />: | |||
* ''R<sub>max</sub>'' is the maximum value of ''R'' along the LCFS or separatrix. | |||
* ''R<sub>min</sub>'' is the minimum value of ''R'' along the LCFS or separatrix. | |||
* ''Z<sub>max</sub>'' is the maximum value of ''Z'' along the LCFS or separatrix. | |||
* ''Z<sub>min</sub>'' is the minimum value of ''Z'' along the LCFS or separatrix. | |||
* ''a'' is the minor radius of the plasma, defined as ''(R<sub>max</sub> - R<sub>min</sub>)/2''. | |||
The ellipticity is then defined as follows: | |||
:<math> \kappa = (Z_{max}-Z_{min})/2a</math> | |||
Higher elongation is beneficial for fusion performance, but comes with increased vertical instability growth rate and thus increased risk of vertical displacement event (VDE) type disruptions.<ref>D.A. Humphreys, et al., ''Experimental vertical stability studies for ITER performance and design guidance'' [[doi:10.1088/0029-5515/49/11/115003|Nucl. Fusion '''49''' (2009) 115003]]</ref> | |||
Because of vertical stability constraints, <math>\kappa</math> is usually limited to a value close to about 1.8. | |||
== See also == | == See also == | ||
| Line 8: | Line 20: | ||
* [[Toroidal coordinates]] | * [[Toroidal coordinates]] | ||
* [[Effective plasma radius]] | * [[Effective plasma radius]] | ||
== References == | |||
<references /> | |||
Latest revision as of 22:47, 30 March 2023
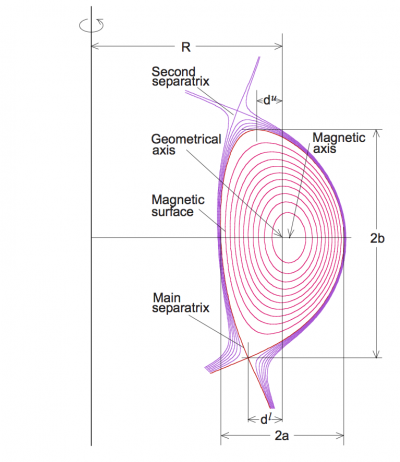
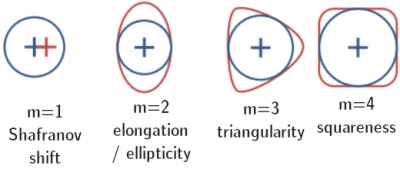
The ellipticity (also referred to as elongation[1]) refers to the shape of the poloidal cross section of the Last Closed Flux surface or separatrix of a tokamak.
Assuming[1]:
- Rmax is the maximum value of R along the LCFS or separatrix.
- Rmin is the minimum value of R along the LCFS or separatrix.
- Zmax is the maximum value of Z along the LCFS or separatrix.
- Zmin is the minimum value of Z along the LCFS or separatrix.
- a is the minor radius of the plasma, defined as (Rmax - Rmin)/2.
The ellipticity is then defined as follows:
Higher elongation is beneficial for fusion performance, but comes with increased vertical instability growth rate and thus increased risk of vertical displacement event (VDE) type disruptions.[2] Because of vertical stability constraints, is usually limited to a value close to about 1.8.
See also
References
- ↑ 1.0 1.1 T.C. Luce, Plasma Phys. Control. Fusion 55 (2013) 095009
- ↑ D.A. Humphreys, et al., Experimental vertical stability studies for ITER performance and design guidance Nucl. Fusion 49 (2009) 115003