Ellipticity: Difference between revisions
Jump to navigation
Jump to search
(added expression "elongation") |
(Mention the effects of increasing elongation) |
||
| Line 10: | Line 10: | ||
The ellipticity is then defined as follows: | The ellipticity is then defined as follows: | ||
:<math> \kappa = (Z_{max}-Z_{min})/2a</math> | :<math> \kappa = (Z_{max}-Z_{min})/2a</math> | ||
Higher elongation is beneficial for fusion performance, but comes with increased vertical instability growth rate and thus increased risk of vertical displacement event (VDE) type disruptions.<ref>D.A. Humphreys, et al., ''Experimental vertical stability studies for ITER performance and design guidance'' [[doi:10.1088/0029-5515/49/11/115003|Nucl. Fusion '''49''' (2009) 115003]]</ref> | |||
== See also == | == See also == | ||
Revision as of 19:40, 27 March 2023
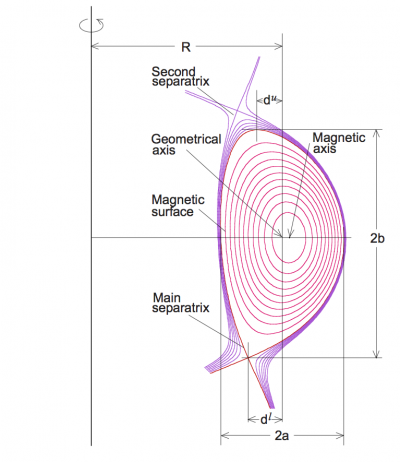
The ellipticity (also referred to as elongation[1]) refers to the shape of the poloidal cross section of the Last Closed Flux surface or separatrix of a tokamak.
Assuming[1]:
- Rmax is the maximum value of R along the LCFS or separatrix.
- Rmin is the minimum value of R along the LCFS or separatrix.
- Zmax is the maximum value of Z along the LCFS or separatrix.
- Zmin is the minimum value of Z along the LCFS or separatrix.
- a is the minor radius of the plasma, defined as (Rmax - Rmin)/2.
The ellipticity is then defined as follows:
Higher elongation is beneficial for fusion performance, but comes with increased vertical instability growth rate and thus increased risk of vertical displacement event (VDE) type disruptions.[2]
See also
References
- ↑ 1.0 1.1 T.C. Luce, Plasma Phys. Control. Fusion 55 (2013) 095009
- ↑ D.A. Humphreys, et al., Experimental vertical stability studies for ITER performance and design guidance Nucl. Fusion 49 (2009) 115003