Triangularity: Difference between revisions
Jump to navigation
Jump to search
No edit summary |
|||
| Line 1: | Line 1: | ||
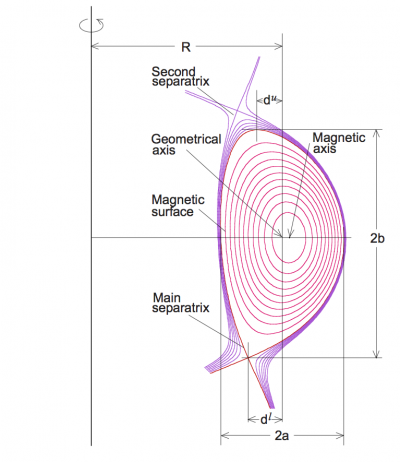
[[File:Geometry.png|400px|thumb|right|Sketch of tokamak geometry, including separatrix]] | |||
The triangularity refers to the shape of the poloidal cross section of the Last Closed [[Flux surface]] (LCFS) or [[separatrix]] of a [[tokamak]]. | The triangularity refers to the shape of the poloidal cross section of the Last Closed [[Flux surface]] (LCFS) or [[separatrix]] of a [[tokamak]]. | ||
Assuming: | Assuming: | ||
* ''R<sub>0</sub>'' is the major radius of the midpoint of the 2 intersections of the LCFS or separatrix with the equatorial plane (''Z'' = 0). | * ''R<sub>0</sub>'' is the major radius of the midpoint of the 2 intersections of the LCFS or separatrix with the equatorial plane (''Z'' = 0). | ||
* ''a'' is the minor radius of the plasma, defined as the radial difference between the 2 intersections of the LCFS or separatrix with the equatorial plane (''Z'' = 0), divided by 2. | * ''a'' is the minor radius of the plasma, defined as the radial difference between the 2 intersections of the LCFS or separatrix with the equatorial plane (''Z'' = 0), divided by 2. | ||
* ''R<sub> | * ''R<sub>upper</sub>'' is the major radius of the upper X-point (in case it exists) or of the highest vertical point of the LCFS. | ||
* ''R<sub> | * ''R<sub>lower</sub>'' is the major radius of the lower X-point (in case it exists) or of the lowest vertical point of the LCFS. | ||
The upper triangularity is then defined as follows: | The upper triangularity is then defined as follows: | ||
:<math> \delta_{ | :<math> \delta_{upper} = (R_0-R_{upper})/a</math> | ||
and similar for δ<sub> | and similar for δ<sub>lower</sub>. | ||
The overall triangularity is defined as the mean of δ<sub> | The overall triangularity is defined as the mean of δ<sub>upper</sub> and δ<sub>lower</sub>. | ||
== See also == | == See also == | ||
Revision as of 11:59, 12 June 2014
The triangularity refers to the shape of the poloidal cross section of the Last Closed Flux surface (LCFS) or separatrix of a tokamak. Assuming:
- R0 is the major radius of the midpoint of the 2 intersections of the LCFS or separatrix with the equatorial plane (Z = 0).
- a is the minor radius of the plasma, defined as the radial difference between the 2 intersections of the LCFS or separatrix with the equatorial plane (Z = 0), divided by 2.
- Rupper is the major radius of the upper X-point (in case it exists) or of the highest vertical point of the LCFS.
- Rlower is the major radius of the lower X-point (in case it exists) or of the lowest vertical point of the LCFS.
The upper triangularity is then defined as follows:
and similar for δlower. The overall triangularity is defined as the mean of δupper and δlower.