TJ-II:Tomography
A tomography program has been developed at TJ-II for the reconstruction of the local emission of radiation from a set of line-integrated measurements in a single poloidal plane (φ = constant). The local emission E is expressed as a function of the vacuum flux coordinates (ρ,θ) (from VMEC) in the form of a series expansion:
Separating out the m = 0 terms:
For an optimal reconstruction process, one would like the expansion functions to form an orthogonal set (thus avoiding statistical collinearities). The orthogonality should apply with respect to the area integral, since this is what contributes to the measured emission. This leads to:
where δij is the Kronecker delta. The Fourier-Bessel functions satisfy this requirement.
The reconstruction algorithm
The local emission E(ρ,θ) is calculated on a sufficiently fine grid (ρi,θj), i = 1,...,Nρ, j = 1,...,Nθ. The emission of a grid element (with area daij) to detector number ν is evaluated taking into account the distance dνij of the grid element (i,j) to the detector:
Of course, only grid elements lying inside the detector beam viewing angle are contemplated; this is expressed by the factor δνij which equals 1 when the grid element lies inside the beam, and 0 otherwise (partial overlap between the viewing beam and the grid element is not contemplated since the grid is assumed to be sufficiently fine). By integrating over all grid elements (i,j), the total emission received by detector ν, Iν can be calculated.
Since the local emission E(ρ,θ) is expanded as a series, this integration can be performed for each mode separately. Labeling the modes (n,m) by a single index μ, we can write the relation between mode amplitudes and detected intensities as:
where the Cμ are the mode coefficients. This is a linear set of equations that can be solved using standard techniques, allowing fast recovery of the mode coefficients from the detector signals. The detector signals Iν are assigned weights wν inversely proportional to the square of the measurement error of measurement Iν. Thus, any channel ν can be excluded from contributing to the result by setting wν = 0.
The regression technique used is a combined Gauss-Newton and modified Newton gradient descent algorithm that minimizes both the reconstruction error and the mode amplitudes.[1]
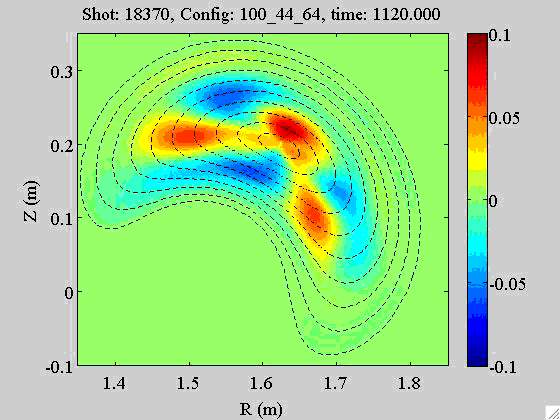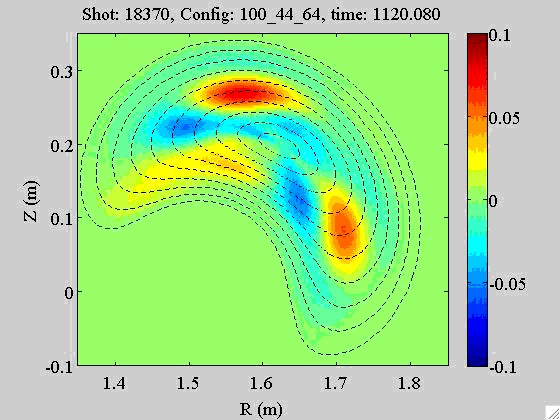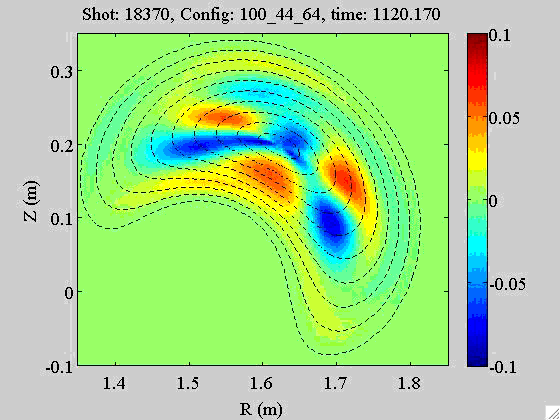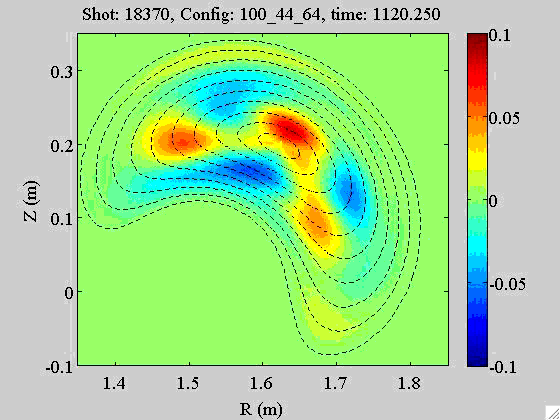
An example
The rotation of an m = 3 mode (or magnetic island) observed by applying the above reconstruction algorithm to the high-pass filtered multichannel bolometry signals at TJ-II:
See also
References
- ↑ J.A. Alonso, J.L. Velasco, I. Calvo, T. Estrada, J.M. Fontdecaba, J.M. García-Regaña, J. Geiger, M. Landreman, K.J. McCarthy, F. Medina, B.Ph. Van Milligen, M.A. Ochando, F.I. Parra, the TJ-II Team and the W-X Team, Parallel impurity dynamics in the TJ-II stellarator, Plasma Phys. Control. Fusion 58 (2016) 074009