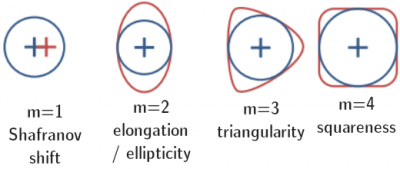
Triangularity

The triangularity refers to the shape of the poloidal cross section of the Last Closed Flux surface (LCFS) or separatrix of a tokamak. Assuming:

• R_max is the maximum value of R along the LCFS or separatrix.
• R_min is the minimum value of R along the LCFS or separatrix.
• R_geo is the geometric major radius, defined as (R_max + R_min)/2.
• a is the minor radius of the plasma, defined as (R_max - R_min)/2.
• R_upper is the major radius of the highest vertical point of the LCFS or separatrix.
• R_lower is the major radius of the lowest vertical point of the LCFS or separatrix.

Sketch of tokamak geometry, including separatrix

Illustration of the m=1,2,3, and 4 perturbations to a tokamak plasma cross section. Triangularity is the m=3 perturbation.

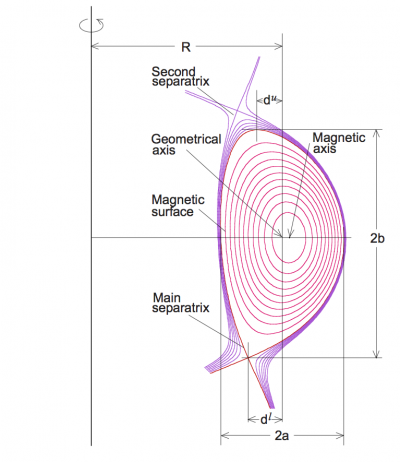
The upper triangularity is then defined as follows:

$\delta _{upper}=(R_{geo}-R_{upper})/a$

and similar for δ_lower. The overall triangularity is defined as the mean of δ_upper and δ_lower.

Triangularity, especially the triangularity opposite the dominant X-point (so upper triangularity for a lower null plasma), influences the stability and character of the pedestal and ELMs.

Some devices (TCV and DIII-D) can form plasma cross sections with negative triangularity (the X-points are pushed to larger $R$ than the center of the plasma), which makes H-mode difficult or impossible to access but improves performance of the L-mode.

See also

• Ellipticity
• Toroidal coordinates
• Effective plasma radius