Toroidal coordinates

Coordinate systems used in toroidal systems:

A toroidal coordinate system

Cartesian

(X, Y, Z)

Cylindrical

(R, φ, Z), where

• R² = X² + Y², and
• tan φ = Y/X.

φ is called the toroidal angle (and not the cylindrical angle, at least not in the context of magnetic confinement).

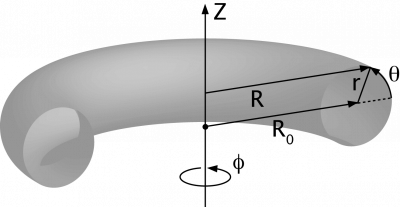
Simple toroidal

(r, φ, θ), where

• R = R₀ + r cos θ, and
• Z = r sin θ

R₀, corresponding to the torus axis, is called the major radius and r the minor radius. θ is called the poloidal angle.

Toroidal

(ζ, η, φ), where

$R=R_{p}{\frac {\sinh \zeta }{\cosh \zeta -\cos \eta }}$

$Z=R_{p}{\frac {\sin \eta }{\cosh \zeta -\cos \eta }}$

where R_p is the pole of the coordinate system. Surfaces of constant ζ are tori with major radii R = R_p/tanh ζ and minor radii r = R_p/sinh ζ. At R = R_p, ζ = ∞, while at infinity and at R = 0, ζ = 0. The coordinate η is a poloidal angle and runs from 0 to 2π. This system is orthogonal.

Magnetic

All of the above coordinate systems are fixed. By contrast, magnetic coordinates adapt to the magnetic field, and therefore to the MHD equilibrium (also see Flux surface). Magnetic coordinates simplify the description of the magnetic field.

• Hamada coordinates. In these coordinates, both the field lines and current lines corresponding to the MHD equilibrium are straight.
• Boozer coordinates. In these coordinates, the field lines corresponding to the MHD equilibrium are straight.