Beta: Difference between revisions
m Updated references |
m Corrected Freidberg |
||
| Line 1: | Line 1: | ||
Plasma performance is often expressed in terms of beta (<math>\beta</math>), defined as: | Plasma performance is often expressed in terms of beta (<math>\beta</math>), defined as: | ||
<ref>J.P. Freidberg, ''Plasma physics and fusion energy'', Cambridge University Press (2007) ISBN 0521851076</ref> | <ref name="freidberg">J.P. Freidberg, ''Plasma physics and fusion energy'', Cambridge University Press (2007) ISBN 0521851076</ref> | ||
:<math>\beta = \frac{\left \langle p \right \rangle}{B^2/2\mu_0}</math> | :<math>\beta = \frac{\left \langle p \right \rangle}{B^2/2\mu_0}</math> | ||
| Line 18: | Line 18: | ||
where <math>B_T</math> is the toroidal magnetic field in T, <math>a</math> is the minor radius in m, and <math>I_p</math> is the plasma current in MA. | where <math>B_T</math> is the toroidal magnetic field in T, <math>a</math> is the minor radius in m, and <math>I_p</math> is the plasma current in MA. | ||
The value of <math>\beta_N</math> has been determined numerically by Troyon to 0.028. Often <math>\beta</math> is expressed in percent, in which case <math>\beta_N = 2.8</math>. This limit results from many different numerical studies determined to find the overall <math>\beta</math> limit out of many different MHD instabilities, such as [[external kink modes]], [[ballooning kink modes]], [[internal modes]], [[localized modes]], etc. <ref | The value of <math>\beta_N</math> has been determined numerically by Troyon to 0.028. Often <math>\beta</math> is expressed in percent, in which case <math>\beta_N = 2.8</math>. This limit results from many different numerical studies determined to find the overall <math>\beta</math> limit out of many different MHD instabilities, such as [[external kink modes]], [[ballooning kink modes]], [[internal modes]], [[localized modes]], etc. <ref name="freidberg"></ref> <br> | ||
Empirical evaluation from the data of different tokamaks raises this value slightly to <math>\beta_N = 3.5</math>, although significantly higher values have been achieved. | Empirical evaluation from the data of different tokamaks raises this value slightly to <math>\beta_N = 3.5</math>, although significantly higher values have been achieved. | ||
<ref>S.A. Sabbagh et al, ''Resistive wall stabilized operation in rotating high beta NSTX plasmas'', [[doi:10.1088/0029-5515/46/5/014|Nucl. Fusion '''46''' (2006) 635-644]]</ref> | <ref>S.A. Sabbagh et al, ''Resistive wall stabilized operation in rotating high beta NSTX plasmas'', [[doi:10.1088/0029-5515/46/5/014|Nucl. Fusion '''46''' (2006) 635-644]]</ref> | ||
Revision as of 08:05, 20 April 2015
Plasma performance is often expressed in terms of beta (), defined as: [1]
i.e., the ratio of the plasma pressure to the magnetic pressure. Here, is the mean plasma pressure, and the mean total field strength. It is customary to introduce also the poloidal beta and the toroidal beta , in which is replaced by the poloidal and toroidal magnetic field component, respectively. One has:
Normalized beta, beta limit
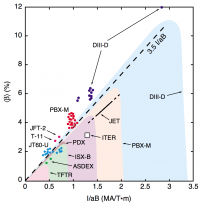
is often expressed in terms of the normalized beta (or Troyon factor)[3], an operational parameter indicating how close the plasma is to reaching the Greenwald limit or a destabilising major MHD activity. Its definition is (for tokamaks): [4]
where is the toroidal magnetic field in T, is the minor radius in m, and is the plasma current in MA.
The value of has been determined numerically by Troyon to 0.028. Often is expressed in percent, in which case . This limit results from many different numerical studies determined to find the overall limit out of many different MHD instabilities, such as external kink modes, ballooning kink modes, internal modes, localized modes, etc. [1]
Empirical evaluation from the data of different tokamaks raises this value slightly to , although significantly higher values have been achieved.
[5]
See also
References
- ↑ 1.0 1.1 J.P. Freidberg, Plasma physics and fusion energy, Cambridge University Press (2007) ISBN 0521851076
- ↑ ITER Physics Expert Group on Disruptions, Plasma Control, and MHD, ITER Physics Basis Chapter 3: MHD stability, operational limits and disruptions, Nucl. Fusion 39 (1999) 2251-2389
- ↑ F. Troyon, R. Gruber, H. Saurenmann, S. Semenzato and S. Succi, MHD-Limits to Plasma Confinement, Plasma Phys. Control. Fusion 26 (1984) 209
- ↑ K. Miyamoto, Plasma Physics and Controlled Nuclear Fusion, Springer-Verlag (2005) ISBN 3540242171
- ↑ S.A. Sabbagh et al, Resistive wall stabilized operation in rotating high beta NSTX plasmas, Nucl. Fusion 46 (2006) 635-644