Flux surface

A given smooth surface S with normal n is a flux surface of a smooth vector field B when

${\vec {B}}\cdot {\vec {n}}=0$

everywhere. It is then possible to define a scalar flux function (f) such that its value is constant on the surface S, and

${\vec {B}}\cdot {\vec {\nabla }}f=0$

In three dimensions, the only closed flux surface corresponding to a non-vanishing vector field is a topological toroid. This fact lies at the basis of the design of magnetic confinement devices.

Assuming the flux surfaces have this toroidal topology, the function f defines a set of nested surfaces, so it makes sense to use this function to label the flux surfaces, i.e., f may be used as a "radial" coordinate. Each toroidal surface f encloses a volume V(f). The surface corresponding to an infinitesimal volume V is essentially a line that corresponds to the toroidal axis (called magnetic axis when B is a magnetic field).

The flux F through an arbitrary surface S is given by

$F=\int _{S}{{\vec {B}}\cdot {\vec {n}}dS}$

Diagram showing the surfaces defining the poloidal (red) and toroidal (blue) flux

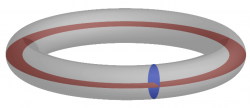
When B is a magnetic field with toroidal nested flux surfaces, two magnetic fluxes can be defined from two corresponding surfaces. The poloidal flux is defined by

$\psi =\int _{S_{p}}{{\vec {B}}\cdot {\vec {n}}dS}$

where S_p is a ring-shaped ribbon stretched between the magnetic axis and the flux surface f, and the toroidal flux by

$\phi =\int _{S_{t}}{{\vec {B}}\cdot {\vec {n}}dS}$

where S_t is a poloidal section of the flux surface. It is natural to use ψ or φ to label the flux surfaces instead of the unphysical label f.

See also

• MHD equilibrium
• Magnetic shear
• Effective plasma radius