Flux tube: Difference between revisions
No edit summary |
No edit summary |
||
| (One intermediate revision by the same user not shown) | |||
| Line 16: | Line 16: | ||
</math> | </math> | ||
This has the important consequence that a given volume of plasma contained within a flux tube ''remains'' inside the flux tube as it is advected, twisted, and stretched by the fluid flow. | This has the important consequence that a given volume of plasma contained within a flux tube ''remains'' inside the flux tube as it is advected, twisted, and stretched by the fluid flow. | ||
<ref | <ref>A. Dinklage, ''Plasma physics: confinement, transport and collective effects'', Vol. 670 of Lecture notes in physics, Springer (2005) {{ISBN|3540252746}}</ref> | ||
<ref | <ref>W.D. D'haeseleer et al, ''Flux coordinates and Magnetic Field Structure'', Springer-Verlag {{ISBN|3-540-52419-3}}</ref> | ||
This implies that the topology of the flux tube cannot change due to the fluid flow. | This implies that the topology of the flux tube cannot change due to the fluid flow. | ||
Stated differently, the magnetic flux contained in a volume element of the plasma is carried along unchanged as the element moves. | Stated differently, the magnetic flux contained in a volume element of the plasma is carried along unchanged as the element moves. | ||
| Line 28: | Line 28: | ||
== References == | == References == | ||
<references | <references /> | ||
Latest revision as of 11:29, 26 January 2023
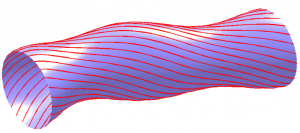
A flux tube is a region of space bounded by a flux surface, i.e., a surface such that the magnetic field is everywhere perpendicular to the surface normal.
In flux coordinates, such a surface has cylindrical topology. In a closed magnetic field region, the topology is toroidal.
The magnetic flux traversing any cross sectional area of a flux tube is invariant.
Contrary to magnetic islands, that are bounded by a separatrix, there is not necessarily any essential dynamical difference between the regions inside and outside of a flux tube.
Flux conservation
In the framework of Ideal Magneto-Hydrodynamics, the MHD kinematic equation reads (in the perfectly conducting limit, ):
This has the important consequence that a given volume of plasma contained within a flux tube remains inside the flux tube as it is advected, twisted, and stretched by the fluid flow. [1] [2] This implies that the topology of the flux tube cannot change due to the fluid flow. Stated differently, the magnetic flux contained in a volume element of the plasma is carried along unchanged as the element moves. Also, two plasma elements connected by a field line will always remain connected by that same field line as the plasma flows. This is sometimes known as the Frozen Flux Hypothesis.
See also
References
- ↑ A. Dinklage, Plasma physics: confinement, transport and collective effects, Vol. 670 of Lecture notes in physics, Springer (2005) ISBN 3540252746
- ↑ W.D. D'haeseleer et al, Flux coordinates and Magnetic Field Structure, Springer-Verlag ISBN 3-540-52419-3