Flux surface: Difference between revisions
No edit summary |
No edit summary |
||
| Line 11: | Line 11: | ||
This fact lies at the basis of the design of magnetic confinement devices. | This fact lies at the basis of the design of magnetic confinement devices. | ||
The function ''f'' defines a set of ''nested'' surfaces, so it makes sense to use this function to label the flux surfaces, i.e., ''f'' may be used as an effective "radial" coordinate. Each toroidal surface ''f'' encloses a volume ''V(f)''. | |||
The surface corresponding to an infinitesimal volume ''V'' is essentially a line that corresponds to | The surface corresponding to an infinitesimal volume ''V'' is essentially a line that corresponds to | ||
the ''toroidal axis'' (called ''magnetic axis'' when ''B'' is a magnetic field). | the ''toroidal axis'' (called ''magnetic axis'' when ''B'' is a magnetic field). | ||
Revision as of 18:01, 19 August 2009
A given smooth surface S with normal n is a flux surface of a smooth vector field B when
everywhere. Defining a scalar flux function (f) such that its value is constant on the surface S, this can be rewritten
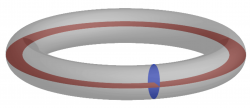
In three dimensions, the only closed flux surface corresponding to a non-vanishing vector field is a topological toroid. [1] This fact lies at the basis of the design of magnetic confinement devices.
The function f defines a set of nested surfaces, so it makes sense to use this function to label the flux surfaces, i.e., f may be used as an effective "radial" coordinate. Each toroidal surface f encloses a volume V(f). The surface corresponding to an infinitesimal volume V is essentially a line that corresponds to the toroidal axis (called magnetic axis when B is a magnetic field).
The flux F through an arbitrary surface S is given by
When B is a magnetic field with toroidal nested flux surfaces, two magnetic fluxes can be defined from two corresponding surfaces. [2] The poloidal flux is defined by
where Sp is a ring-shaped ribbon stretched between the magnetic axis and the flux surface f, and the toroidal flux by
where St is a poloidal section of the flux surface. It is natural to use ψ or φ to label the flux surfaces instead of the unphysical label f.
See also
References
- ↑ The Poincaré-Hopf Theorem.
- ↑ R.D. Hazeltine, J.D. Meiss, Plasma Confinement, Courier Dover Publications (2003) ISBN 0486432424