Flux tube: Difference between revisions
No edit summary |
|||
| Line 11: | Line 11: | ||
== Flux conservation == | == Flux conservation == | ||
In the framework of [[Ideal Magneto-Hydrodynamics]], the MHD kinematic equation reads: | In the framework of [[Ideal Magneto-Hydrodynamics]], the MHD kinematic equation reads (in the perfectly conducting limit, <math>\sigma \to \infty</math>): | ||
:<math> | :<math> | ||
\frac{\partial \vec B}{\partial t} = \vec \nabla \times (\vec v \times \vec B) | \frac{\partial \vec B}{\partial t} = \vec \nabla \times (\vec v \times \vec B) | ||
| Line 17: | Line 17: | ||
This has the important consequence that a given volume of plasma contained within a flux tube ''remains'' inside the flux tube as it is advected, twisted, and stretched by the fluid flow. | This has the important consequence that a given volume of plasma contained within a flux tube ''remains'' inside the flux tube as it is advected, twisted, and stretched by the fluid flow. | ||
<ref>A. Dinklage, ''Plasma physics: confinement, transport and collective effects'', Vol. 670 of Lecture notes in physics, Springer (2005) ISBN 3540252746</ref> | <ref>A. Dinklage, ''Plasma physics: confinement, transport and collective effects'', Vol. 670 of Lecture notes in physics, Springer (2005) ISBN 3540252746</ref> | ||
<ref>W.D. D'haeseleer et al, ''Flux coordinates and Magnetic Field Structure'', Springer-Verlag ISBN 3-540-52419-3</ref> | |||
This implies that the topology of the flux tube cannot change due to the fluid flow. | This implies that the topology of the flux tube cannot change due to the fluid flow. | ||
Stated differently, the magnetic flux contained in a volume element of the plasma is carried along unchanged as the element moves. | Stated differently, the magnetic flux contained in a volume element of the plasma is carried along unchanged as the element moves. | ||
Also, two plasma elements connected by a field line will always remain connected by that same field line as the plasma flows. | Also, two plasma elements connected by a field line will always remain connected by that same field line as the plasma flows. | ||
This is sometimes known as the ''Frozen | This is sometimes known as the ''Frozen Flux Hypothesis''. | ||
== See also == | == See also == | ||
Revision as of 11:14, 22 August 2011
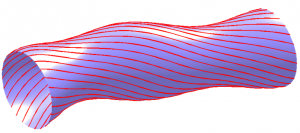
A flux tube is a region of space bounded by a flux surface, i.e., a surface such that the magnetic field is everywhere perpendicular to the surface normal.
In flux coordinates, such a surface has cylindrical topology. In a closed magnetic field region, the topology is toroidal.
The magnetic flux traversing any cross sectional area of a flux tube is invariant.
Contrary to magnetic islands, that are bounded by a separatrix, there is not necessarily any essential dynamical difference between the regions inside and outside of a flux tube.
Flux conservation
In the framework of Ideal Magneto-Hydrodynamics, the MHD kinematic equation reads (in the perfectly conducting limit, ):
This has the important consequence that a given volume of plasma contained within a flux tube remains inside the flux tube as it is advected, twisted, and stretched by the fluid flow. [1] [2] This implies that the topology of the flux tube cannot change due to the fluid flow. Stated differently, the magnetic flux contained in a volume element of the plasma is carried along unchanged as the element moves. Also, two plasma elements connected by a field line will always remain connected by that same field line as the plasma flows. This is sometimes known as the Frozen Flux Hypothesis.